Experience Trading
on the Go
on the Go

‘It’s not whether you’re right or wrong that’s important, but how much money you make when you’re right and how much you lose when you’re wrong’—George Soros
‘Frankly, I don’t see markets; I see risks, rewards, and money’—Larry Hite
A key factor behind Forex trading success is an appropriate balance between risk and reward—a balance relevant to the trading system (or trading strategy) applied.
At its core, a risk-reward ratio quantifies risk versus prospective reward on a trade (potential profit for every dollar risked). It is a measure that profitable traders employ while some newer traders may only pay lip service to.
The fundamental goal of any trader in the Forex market (or any financial market) should be risk management: actions to protect against the downside of a trade.
Risk management includes aspects such as leverage, adherence to a trading system’s rules of engagement, the correct use of protective stop-loss orders, leverage, as well as a system’s risk-reward ratio and trading expectancy.

Risk-Reward Ratio (RRR) = (Take-Profit [TP]-Entry) / (Entry-Stop Loss)
(Note the above points should be detailed in a trading plan—often a blend of fundamental and technical analysis).
To help explain the mechanics behind a risk-reward ratio, figure 1.A shows the EUR/USD (major currency pair) H4 timeframe with a straightforward swing support-turned resistance level applied at $1.2213.
The first step is to define entry. The entry, in the case of figure 1.A, is at $1.2213—the support-turned resistance level.
The second step involves arranging a location for a protective stop-loss order to help limit risk (this is the potential loss on the trade). Naturally, this practice is trader dependent. In figure 1.A, nevertheless, the example places the stop-loss order conservatively: above the high $1.2284 at $1.2286. This is 73 pips.
The final step requires a take-profit objective. Dependent on the trading system employed, multiple take-profit targets may be included. Figure 1.A, based on price action, selected demand located at $1.2039/$1.2068, a downside objective that provided a reasonable risk-reward ratio:
Risk-Reward Ratio = (Take Profit [1.2068]-Entry [1.2213]) / (Entry [1.2213]-Stop Loss [1.2286]) = (approximately) 1:2
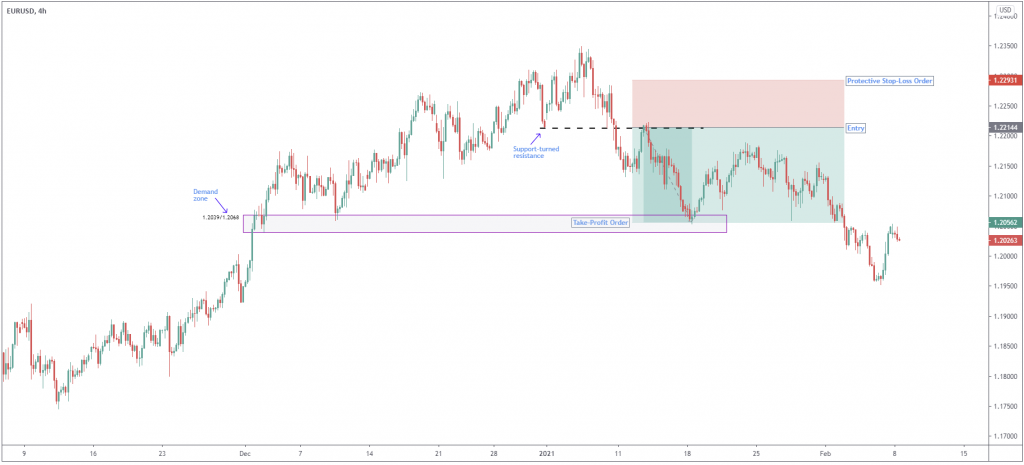
(Figure 1.A: EUR/USD H4 Chart Provided by Trading View)
Many claim a minimum of a 1:2 risk reward ratio is needed to achieve success in the financial markets.
While a healthy risk-reward ratio is desired, traders must also take into consideration their win-loss ratio. As its name implies, a win-loss ratio indicates the total number of winning trades to the total number of losing trades—a metric traders often place much emphasis on. To calculate this, divide total winners by total losing trades (50 winning trades / 100 losing trades = 0.5 [or 50 percent]).
Say a trader usually works with a 1:2 risk-reward ratio (for every dollar risked you make two dollars), but the win-loss ratio is 20 percent. That means for every ten trades, the trader wins two trades and loses eight. Imagine risk per trade is 100 USD and the gain is 200 USD, this equates to a 400 USD loss despite a reasonably attractive risk-reward ratio. To achieve profitability in this case, the strategy requires either a 40 percent win-loss ratio or a higher risk-reward ratio.
So, while a healthy risk-reward ratio is important, the win-loss ratio must also be accounted for.
Trading expectancy refers to what a trader can expect from a strategy over a SERIES of trades (per dollar risked).
Based on Van K. Tharpe’s book: Trade Your Way to Financial Freedom, Tharp states that few people who are actively involved in the markets even know what expectancy means. Even fewer people understand the implications of designing a system around expectancy.
Note that the majority of this segment’s material is derived from Tharp’s aforementioned book.
Tharp also goes on to write that one of the real secrets of trading success is to think in terms of reward-to-risk ratios. Similarly, the first key to understanding expectancy is to think of your trades in terms of their reward-to-risk ratio.
To establish expectancy, you must first determine the risk on a trade—the difference between entry and stop-loss. Tharp refers to this as R. Generally, most traders interpret this as initial risk on a trade: 100 USD, for example. This enables traders to express profit and loss as a ratio of R. An example might be a trade with 1R risk of 100 USD which returns 200 USD on winning trades, on average: a 2R return—a R multiple of 2. The same is said for losses. A 1.5R loss reveals the trader lost 50 percent more than initial risk value (this can happen if price gaps over the protective stop-loss order), while a 0.5R loss equates to only a 50 percent loss of initial risk.
It is important to understand that trading expectancy is measured over a sample of trades. Tharp recommends at least 30 trades to be statically significant, though you should aim for between 100 to 200 trades for a clear picture. When you have a series of profits and losses expressed as risk-reward ratios, you have what Tharp refers to as R-multiple distribution.

By amassing a collection of trades, you have sufficient data to estimate how much a trading system makes over a given number of trades.
Calculation:
Expectancy = (Average Winner x Win Rate) – (Average Loser x Loss Rate)
Scenario 1:
Trader A has a trading system with 200 data samples to work with.
The system, on average, produces a 60 percent win-loss ratio. On winning trades, the system typically returns at least an R multiple of 2. R, in this case, is 100 USD (static position size).
Average winner: 200 USD
Average Loser: 100 USD
Percentage Trade Win: 60 percent
Gross Expectancy: 80 USD (200 USD x 0.60) – (100 x 0.40)
Therefore, on average, Trader A’s system (ignoring commissions) is expected to make 80 USD per trade. In terms of R multiples, this is 0.8R per trade. This is a system with high positive expectancy.
Scenario 2:
Trader B has a trading system with 500 data samples to work with.
The system, on average, produces a 40 percent win-loss ratio. On winning trades, the system typically returns at least an R multiple of 2. R, in this case, is 100 USD (static position size).
Average winner: 200 USD
Average Loser: 100 USD
Percentage Trade Win: 40 percent
Gross Expectancy: 20 USD (200 USD x 0.40) – (100 x 0.60)
On average, over many trades, Trader B’s system (ignoring commissions) is expected to make 20 USD per trade. In terms of R multiples, this is 0.2R per trade. This is a system with positive expectancy.
Scenario 3:
Trader C has a trading system with 100 data samples to work with.
The system, on average, produces a 40 percent win-loss ratio. On winning trades, the system typically returns at least an R multiple of 1.5. R, in this case, is 100 USD (static position size).
Average winner: 150 USD
Average Loser: 100 USD
Percentage Trade Win: 40 percent
Gross Expectancy: USD (150 USD x 0.40) – (100 x 0.60)
On average, over many trades, Trader C’s system (ignoring commissions) is expected to make 0 USD per trade. In terms of R multiples, this is 0R per trade. This is a system with negative expectancy after factoring in commissions.
Scenario 4:
In cases where R is more complex, which is often the case in real-world FX trading, you must find the mean R multiple (a term coined by Tharp).
Consider the following example over 100 trades, with a risk of 100 USD each trade (R):
Winning trades—
20) 1:2 risk-reward ratio
5) 1:3 risk-reward ratio
5) 1:9 risk-reward ratio
100R
Losing trades—
60) 1:1 risk-reward ratio
10) 1.5:1 risk-reward ratio
75R
To find the expectancy you must total all R multiples and divide this value by the number of trades—the mean R multiple.
The R multiple of all winning trades is 100R while the R multiples of all losing trades is 75R. Therefore, we have a 0.25R expectancy per trade over a series of trades. Or, it can be said, this trading system is expected to make 25 USD per trade, on average.
When trading Forex, traders are often consumed by their winning percentage, overlooking the importance of risk-reward ratio and trading expectancy. Successful traders tend to aim for low risk–high reward trades.
A low win percentage does not always mean less profit. Take scenario 2, Trader B’s system operated with a 0.2R expectancy at a 40 percent win-loss ratio. Though the more complex example (scenario 4) showed a 30 percent win-loss ratio managed to achieve the same expectancy.
Depending on your personal goals and trading objectives, a good expectancy level varies. A 0.2R metric is generally accepted for active trading (think day trading [day trader]), while swing traders and longer-term traders tend to aim for in excess of 0.5R.
 Access 10,000+ financial instruments
Access 10,000+ financial instruments Auto open & close positions
Auto open & close positions News & economic calendar
News & economic calendar Technical indicators & charts
Technical indicators & charts Many more tools included
Many more tools included
By supplying your email you agree to FP Markets privacy policy and receive future marketing materials from FP Markets. You can unsubscribe at any time.
Source - cache | Page ID - 1023